The February Issue of the Journal of Finance made it to the top of my stack, and it has a lot of good articles. The first two especially caught my attention, Who Are the Value and Growth Investors? by Sebastien Bertermeier, Larent Calvet, and Paolo Sodini, and Asset Pricing Without Garbage by Tim Kroencke. A review, followed by more philosophical thoughts.
I Bertermeier, Calvet, and Sodini.
Background: Value stocks (low price to book value) outperform growth stocks (high price to book value). Value stocks all move together — if they fall, they all fall togther — so this is a “factor risk” not an arbitrage opportunity. But who would not want to take advantage of the value factor? This is an enduring puzzle.
Fama and French offered one of the best paragraphs in finance as a suggestion:
One possible explanation is linked to human capital, an important asset for most investors. Consider an investor with specialized human capital tied to a growth firm (or industry or technology). A negative shock to the firm’s prospects probably does not reduce the value of the investor’s human capital; it may just mean that employment in the firm will expand less rapidly. In contrast, a negative shock to a distressed [value] firm more likely implies a negative shock to the value of specialized human capital since employment in the firm is more likely to contract. Thus, workers with specialized human capital in distressed firms have an incentive to avoid holding their firms’ [value] stocks. If variation in distress is correlated across firms, workers in distressed firms have an incentive to avoid the stocks of all distressed firms. The result can be a state-variable risk premium in the expected returns of distressed stocks.
But nobody has seen these investors, who shun value stocks despite their high average return, because value stocks are correlated with those investors’ human capital. Value funds tend not to have many customers who come in, learn about the value/growth premium and factor and say “thanks, I’d like to short value” (Lots want to buy hot growth stocks, but hedging is probably not directly on their minds, and it takes a pretty strong “as if” argument to ignore that)
Enter Bertermeier, Calvet, and Sodini.
we examine value and growth investments in a highly detailed administrative panel that contains the disaggregated holdings and socioeconomic characteristics of all Swedish residents between 1999 and 2007.
Value investors are substantially older, are more likely to be female, have higher financial and real estate wealth, and have lower leverage, income risk, and human capital than the average growth investor. By contrast, men, entrepreneurs, and educated investors are more likely to invest in growth stocks.
over the life cycle, households climb the “value ladder,” that is, gradu- ally shift from growth to value investing as their investment horizons shorten and their balance sheets and human capital evolve.
…we find that a single macroeconomic factor—per-capita national income growth— explains on average 88% of the time-series variation of per-capita income in any given two-digit SIC industry. Households employed in sectors with high exposure to the macroeconomic factor tend to select portfolios of stocks and funds with low value loadings. … Furthermore, we show that cross-sectoral differences in loadings are more pronounced for young households than for mature households, consistent with the intuition that human capital risk is primarily borne by the young. As a result, the value ladder is empirically steeper in more cyclical industries.
…More financially secure households should generally be better able to tolerate investment risk .. Consistent with these predictions, we document that households with high financial wealth, low debt, and low background risk tend to invest their financial wealth aggressively in risky assets and select risky portfolios with a value tilt.
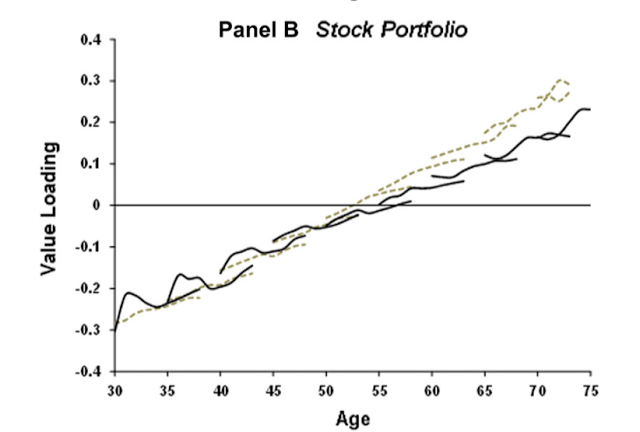
The numbers seem big to me. For example, Figure 2:
Figure 2. The value ladder. The figure plots the value loading of the risky portfolio (Panel A) and the stock portfolio (Panel B) for different cohorts of households. Each solid line corresponds to the average loadings of households in a given cohort, weighted by financial wealth. Each dotted line is the corresponding predicted value loading, obtained by using age, wealth variables, and human capital multiplied by the household-level baseline regression coefficients in Table III. A cohort is defined as a five-year age bin. The first cohort contains households with a head aged between 30 and 34 in 1999, while the oldest cohort has a head aged between 70 and 74 in 1999. The loadings of all households in year t are demeaned to control for changes in the composition of the Swedish stock market. Panel A is based on the panel of all Swedish risky asset market participants and Panel B on the panel of all Swedish direct stockholders over the 1999 to 2007 period.
-0.3 to 0.3 loadings on HML are quite large. Most value mutual funds don’t get that big. (HML is lolg value and short growth)
Overall,
The patterns we uncover appear remarkably consistent with the portfolio implications of risk-based theories.
To be fair, the authors offer behavioral interpretations as well,
we find that sentiment-based explanations of the value premium also help explain the portfolio evidence. Overconfidence, which is more prevalent among men than women (Barber and Odean (2001)), is consistent with the growth tilt of male investors. [JC, yes, but that’s pretty weak. Men and women also have different human capital paths on average.] As attention theory predicts (Barber and Odean (2008)), a majority of direct stockholders hold a small number of popular stocks. Furthermore, some of the portfolio evidence can be explained by complementary risk-based and psychological stories. For instance, the growth tilt of entrepreneurs can be attributed both to exposure to private business risk (Heaton and Lucas (2000), Moskowitz and Vissing-Jørgensen (2002)) and to marked overconfidence in own decision-making skills (Busenitz and Barney (1997))
But I’m interested that all of these are “alternative explanations” of things that also have portfolio interpretations, not puzzling facts that have no portfolio interpretation, which is the usual bread and butter of behavioral finance. (It looks a lot like defense against referees to me!)
II Kroencke:
Background: The main question of asset pricing is, why do some assets reliably earn higher returns, on average, than others? The answer is, compensation for risk. Our benchmark model says this: People in Fall 2008 were really unhappy that just as their jobs and businesses were in trouble, and just as they were cutting back on consumption expenditures, their stock portfolios fell too. How nice it would have been if stocks rose on the occasion, and so could buffer other misfortune. In turn, that means people will, ahead of time, shy away from stocks that are likely to fall more in bad times, lowering their prices and raising their average returns. In sum, our baseline model is
Expected return – risk free rate = (risk aversion coefficient) x (covariance of return with consumption growth)
This model does work, qualitatively. Stocks covary with consumption growth more than bonds. However, the measured covariances are small, so the risk aversion coefficient you need to get this to work is absurdly high — 50 or more. Such people don’t get out of bed in the morning for fear of anvils falling from the sky.
For a long time, — since this model emerged in the early 1980s — we’ve recognized that some of the trouble may lie with measured consumption growth. Kroencke has a good review of the many attempts to get around this project. Two stand out worth mentioning here. Alexi Savov wrote the beautiful Asset Pricing with garbage. More consumption means more garbage, and data on garbage are in some ways (more below) cleaner than data on consumption. The standard model works a lot better using garbage to measure consumption.
Another long time favorite of mine is Ravi Jagannathan and Yong Wang’s “Lazy investors…” paper, which is great except for the title in my opinion. They used fourth quarter to fourth quarter consumption growth rather than the usual monthly consumption growth. Surely asset prices are not driven by who goes up and down at lunch time. Similarly, it only takes a moment’s thought to realize that monthly consumption numbers are poorly measured for this purpose. An especially nice feature of Jagannathan and Wang don’t really make progress on the equity premium. But covariances with fourth quarter to fourth quarter consumption growth explain the value premium nicely, a tougher puzzle really (see above!)
As Korencke puts it
using fourth-quarter to fourth-quarter consumption is a straightforward way to mitigate time-aggregation and to bring the data closer to point consumption growth as well
Now, Kroencke. Your first instinct might be “measurement error,” but that isn’t necessarily a problem
Observable consumption is subject to measurement error, which is uncorrelated with stock market returns. From an asset pricing perspective, observable consumption growth would be eligible to measure the consumption risk of stock returns, that is, should produce unbiased estimates of consumption covariances.
Let me unpack that. Suppose consumption growth has a measurement error uncorrelated with anything. Then
covariance(return, measured consumption growth) = covariance[return, (true consumption growth + measurement error)]
but if measurement error is uncorrelated with everything, it’s also uncorrelated with returns, and
covariance(return, measured consumption growth) = covariance[return, true consumption growth]
So what is the problem? The central insight
However, NIPA statisticians do not attempt to provide a consumption series to measure stock market consumption risk. Instead, they try to estimate the level of consumption as precisely as possible. As a result, they optimally filter observable consumption to generate their series of reported NIPA consumption.
This is a beautiful and deep insight. The problem is not “error.” The problem (pervasive in finance) is that the data are collected for another purpose.
Example: Suppose you are a government statistician, and you are asked to provide numbers on consumption, whose levels are as accurate as possible. You have consumption on Monday = $200, and consumption on Wednesday = $210. You don’t have data for Tuesday. What do you report? $205 of course! That’s the best guess you have of the level of consumption.
But asset pricing demands the growth rate of consumption. And asset pricing is very sensitive about timing. If we shift all consumption measures one period forward or backward in time, the level measurement is not far off. But that destroys the correlation of consumption growth rates with anything else.
This is a pervasive problem in finance. Venture capital, private equity, university endowments or any other institution holding illiquid assets does rightly the same thing. Real estate values have the same problem. Suppose you see a true market value $200 on Monday and $210 on Wednesday. What do you report for Tuesday? Well, $205 of course. That is the best guess of the level of the asset on Tuesday. But a time series of such guesses grossly understates the volatility of the assets, makes returns artificially serially correlated (if you fill in from Monday through Friday, it will seem like a positive return every day), and destroys their correlation or betas with other assets. Beware using numbers for unintended purposes. Beware the Sharpe ratios of illiquid assets.
On top, filtering is intensified by the well-known bias stemming from time-aggregation
NIPA consumption is the total consumption over the month (at best). If you correlate that consumption with asset returns from last day of previous month to last day of this month, you’re making a mistake.
Kroencke “unfilters” consumption data. He uses a nice model of how the BEA filters the data, a more complex version of my Monday-Wednesday example, to make a good guess of what the data looked like before filtering, i.e. what underlying growth rates really are. (You can’t do this in my example, but suppose my example was, you observe Monday $200, Wednesday $210, and you have data for some components but are missing others for Tuesday. To measure growth rates and correlations, you would not use the Monday and Wednesday data as much, and would rely more on the partial observations for Tuesday)
The results?
unfiltered NIPA consumption is able to explain the equity premium together with constant relative risk aversion (CRRA) preferences with a coefficient of relative risk aversion between 19 and 23 in the postwar period (1960–2014),
unfiltered NIPA consumption can explain a substantial fraction of the average returns of decile portfolios sorted by size, book-to-market, and investment growth.
Alas, Kroencke didn’t make any nice average return vs. covariance plots for the blog, so you’ll have to go read the tables.
There is another, rather dramatic point that surfaces early and its impact explained toward the end. Unfiltered consumption data look a lot more like a random walk.
This is the “variance ratio” graph. A random walk has a flat line. An upward sloping line means positive serial correlation — high growth this year is likely to be followed by high growth next year. A downward sloping line means negative serial correlation. The variance ratio is particularly good at detecting long-run unstructured mean reversion.
You knew that filtering would lead to spurious positive serial correlation in consumption growth. How much? All of it!
The random walk in consumption (going back to Bob Hall’s beautiful paper) is a very nice intuitive result. If you know you’re going to be better off in the future, go out to dinner now. Consumption should be like stock prices.
It matters particularly now, in the context of the “long run risks” model, for a very prominent exampleBanal Kiku and Yaron Long run risks. That whole model depends on the idea that long run risks are larger than short run risks, which they infer from the positive serial correlation of consumption growth. If consumption is a random walk, long run risks collapse to power utility. (More in a recent review.)
(To be fair, this criticism addresses the univariate properties of consumption. It is possible for a series to be a random walk in its univariate representation, but forecastable by other variables. Stock returns themselves are a great example, a nearly perfect univariate uncorrelated process, but forecastable by price-dividend ratios. So, the next round of “long run risks” may well find long run consumption growth forecastability from other variables, like P/E ratios.)
Thoughts
Why do I like these papers so much? I guess in part, they confirm my priors. One has to be honest. But that is a terrible reason to like and blog about papers. The blogosphere is full of “studies show that” whatever point one wants to flog today.
I like them because I think they’re well done, and make the case convincingly.
Most of all, I like them because they show how after long and patient work, involving taking data really seriously, phenomena that seem like “puzzles,” needing to be addressed by new and inventive theories, really are not puzzles, and explainable by simple economics.
This is “normal science” at its best. Looking back on the history of science, over and over, observations seemed not to fit good theories, and resulted in hundreds of new and creative “explanations.” Once in a great while those puzzles result in dramatically new theories, which we celebrate. But far more often, after decades, and centuries at times, dogged persistent work showed how indeed things work as you think they might, and the original simple theory was right after all. The “rejections” of the consumption based model started around 1980. It took a long time to see the glass is not completely empty.
Everyone wants to be the “paradigm shifter,” and the journals have about 10 new theories in every issue. Of which 9.99 are soon forgotten.
Part of my psychological makeup, part of what attracted me to economics all along, are the far more frequent cases in which dogged work shows how supply and demand indeed explain all sorts of puzzles.
I like “normal science.” And I think we should celebrate it more.
2017/03/more-good-finance-articles.html